Lessons from the Edge

“The Science of Complexity”

In which Julien Sprott reviewed basic concepts of complexity science, and the similar patterns that can be observed across diverse systems.
Julien Clinton Sprott, PhD, Professor of Physics, University of Wisconsin

• Some characteristics of Dynamical Systems are:
  • The system evolves over time according to a set of rules.
  • The present conditions determine the future.
  • The rules are usually nonlinear – they are random.
  • There may be many interacting variables.
    
    
• Biological sciences are only just beginning to understand this, and social sciences are further behind – they “still believe in free will.”

• Dynamical systems are everywhere. They include:
  
  • The Solar System
  • The atmosphere/ weather
  • The economy/ stock market
  • The human body (itself composed of many dynamical systems)
  • The spread of epidemics
  • The internet

   

There are four forms of Dynamical Systems:

Key points from the chart:

• Complex systems can evolve with simple rules.
  
  
• Most real-world systems fall in the bottom-right quadrant; they seem to develop in a random way, where we can’t predict.

• This is a key issue. Measure any system, and you’ll see variation within a range— even in systems that appear to be regular and stable, such as a heart-beat.
  
  
• Even simple dynamic systems produce chaotic patterns.

• Chaotic systems never repeat their behavior. This makes long-term prediction impossible.
  
  
• Chaotic systems depend sensitively on initial conditions. This is illustrated by the “Butterfly effect,” which suggests that a butterfly flapping its wings in Manila can cause a thunder storm in Houston, Texas.
  
  
• Chaotic systems allow for short-term predictions, but not long-term prediction. For example, we may know that it will be raining tomorrow afternoon, but it is impossible to predict whether it will rain this time next month.
  
  
• Chaos comes and goes with a small change in some “control knob.” Even a slight change in some variable can result in extreme shifts in system behavior.
  
  
• Chaotic systems tend to be fractal. That is, similar structures can be seen at different levels of “magnification.”

• Attractors are points to which movement is pulled. They create “basins” to which behavior is drawn. Imagine a marble coming to rest at the bottom of a bowl – that place is the attractor.
  
  
• Although attractors create unpredictable movement, they also exclude many possibilities.
  
  
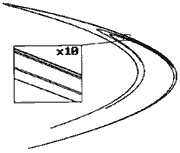
• A pattern created by the “Henon Attractor” is shown to the left. Even though the line seems to cross back over itself, in reality no two points are the same. There is both order and randomness created by the attractor.
  
  
• Attractors are fractal in structure; they can be viewed at infinite levels of detail, and still look the same. (This is shown in the magnified portion of the Henon Attractor visual.)

• Fractal: A geometric image that is self-similar with structure on all scales. The detail persists at all levels.
  
  
• Examples of fractals include:
  • bolt of lightning
  • The leaf of a fern
  • Your body’s vascular system
  • Clouds
  • Planetary rings
  • The coast line of California

• They display emergent behavior. That is, patterns can arise from random beginnings.
  
  
• They display self-organization. Chaos gives rise to order.
  
  
• They evolve.
  
  
• They adapt.
  
  
• They are comprised of autonomous agents.
  
  
• They can learn.
  
  
• They exhibit artificial intelligence.
  
  
• They can die / become extinct.

• “Nature is complicated, but simple models may suffice.”

Copyright © 1999, VHA Inc. Permission
to copy for educational purposes only.